Koers bereik
Voor het antwoord op de vraag welke optie of constructie we gaan kopen of verkopen
is het van belang wat we denken dat het koers verloop is/wordt van de onderliggende waarde.
We gaan in de praktijk vaak uit van een normale kans verdeling, waarbij u in het achterhoofd
moet houden dat de kans verdeling van de onderliggende waarde vaak ook niet -normaal- is verdeeld.
We gaan in dit stukje even uit de dat koers verdeling wel -normaal- is verdeeld.
In dat laatste geval maken we dan vaak gebruik van de Bell Curve.
De bell curve (de normale verdeling of Gaussische kromme) is een wiskundige functie die in de statistiek
vaak wordt gebruikt om de waarschijnlijkheidsverdeling van een variabele te beschrijven
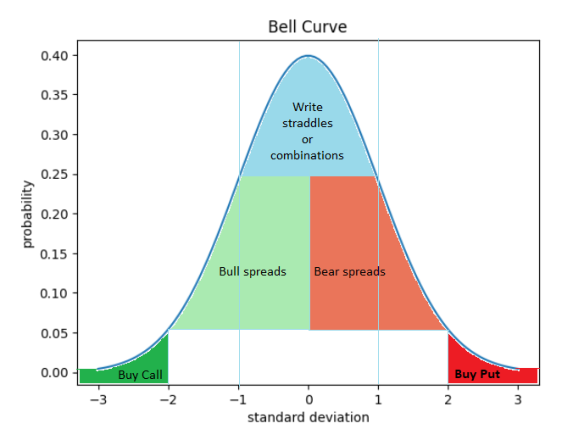
Op investopedia.com komen we de volgende afbeelding van de Bell Curve tegen

Op de horizontale as zien we de standaard deviatie en op de verticale as de waarschijnlijkheid.
Bij 0 standaard deviatie zien we de hoogste waarde, dat is het gemiddelde, the mean.
We zien dat bij een hogere standaard deviatie (zowel + als -) de waarschijnlijkheid afneemt.
Hoe groter de standaard deviatie, des te lager de waarschijnlijkheid.
De meeste punten in een verzameling waar de curve betrekking op heeft zullen dus binnen de
+1sd en -1SD liggen.
.
Ik heb even door Google Colab een Bell curve laten tekenen, dat is wat duidelijker, en is opgebouwd uit
‘echte’ berekende waarden, waarbij mu = 0 (gemiddelde) en sigma =1 (standaard deviatie).

De meeste waarden van de verzameling zullen dus in het groene gebied liggen, minder waarden in het roze gebied
en nog veel minder waarden in het rode gebied.
.
Laten we eens gek doen, en we gooien die curve op z’n kant.
Dat plaatje ziet u hieronder.
.
En stelt u nu zich nu eens voor, dat op standaard deviatie = 0 de slotkoers van de onderliggende waarde van
vandaag ligt.
Wanneer we de tijd even achterwege laten op de horizontale schaal, dan hebben we dus een 68,2%
waarschijnlijkheid (SD+1 en SD-1) dat het koersbereik in het groene gebied ligt.
De waarschijnlijkheid dat deze verder van de mean ( 0 ) gaat afwijken wordt steeds groter naarmate de deviatie
groter wordt.
.
Je kan het groene koersbereik tussen de +1Sd en de -1Sd bekijken als een zijwaartse range waarin de koers
met een waarschijnlijkheid van 68,2% komt te lopen.
.
Een koers welke boven deze waarde in het gebied +1Sd ligt is ‘waarschijnlijk’ te hoog en een koers welke in
het gebied -1Sd ligt is waarschijnlijk te laag.
DIt geldt met een hogere waarschijnlijkheid voor koersen die boven +2Sd of onder -2Sd liggen .
.
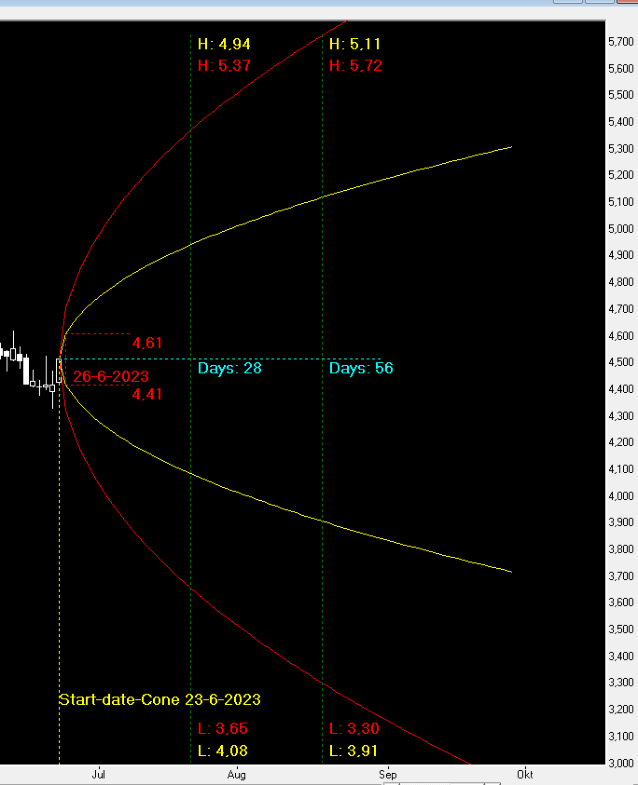
In de praktijk, waarbij we de tijd meenemen ziet dit er bij een fonds als volgt uit.
.

De gele lijn is het verloop met mede name van de tijd bij Sd1 en de rode lijn is bij Sd2.
U herkent natuurlijk het koersverloop van Aegon.
De +1Sd en de -1Sd voor maandag 26-juni-2023 staat weergegeven.
De bogen die het verloop van Sd1 en Sd2 weergeven in combinatie met de komende expiratie
datums staan ook vermeld.
.
Voor we verder gaan moet u goed begrijpen dat de bell curve een probabilistische benadering is.
Het werkelijke koersverloop van de onderliggende waarde is afhankelijk van vele factoren zoals:
marktomstandigheden, bedrijfsprestaties en nieuws gebeurtenissen.
Gebruik van de bell curve geeft dus geen garantie over het bereik waarin het koers verloop waarschijnlijk
komt te liggen.
.
In latere tekst en voorbeelden zult u zien dat ik voor de constructie van de bell curve meestal gebruik
maak van de IV (implied volatility) omdat dit de volatiliteit is die de beleggers verwachten en waarop de
premie van een optie mede gebaseerd is.
In onderstaande tekst gaan we even verder met aandeel ABC, een volatiliteit van X en een koerswaarde
van 100.
Alle gegeven getallen zijn ter illustratie.
.

Op de horizontale as staat de koers weergegeven van het aandeel ABC.
In bovenstaande figuur ziet een oranje lijn die de aanschaf van aandelen weergeeft die gekocht
zijn op het moment van koerswaarde = 100.
De blauwe lijn herkent u als de bell curve, the probability.
Wanneer de koers van ABC gaat stijgen mag er winst worden verwacht.
Hieronder dezelfde figuur waarbij de aanschaf van een Call met strike = 105 is ingetekend.
Voor de eenvoud stellen we de delta op de waarde 1 en de premie op 5.

De premie van deze call is 5, dus er zal een waarde van 105 + 5 = 110 moeten worden overwonnen
voordat er winst wordt gemaakt.
U ziet aan de bell curve al wel dat de verwachting dat deze optie winst gaat opleveren in dit geval laag is.
Het verlies is beperkt tot de betaalde optie premie, terwijl dit bij aanschaf aandelen (oranje lijn) toeneemt
naarmate de koers blijft dalen.
.
Laten we dit eens bekijken voor een call met strike = 90 en premie = 5, wat in onderstaande figuur wordt
weergegeven.

U ziet dat de call met strike = 90 boven de koerswaarde 95 winst oplevert. Wanneer u dat vergelijkt
met het plaatje van de call met strike = 105 ziet u dat de verwachting op de bell curve ook hoger is.
De call met strike-90 heeft dus een hogere winst verwachting dan de call met strike-105.
Laten we dat even bekijken voor een put optie.

Te zien is dat deze put optie winst waarde krijgt wanneer de koers van het aandeel onder de waarde
90 komt (95 -premie).
Laten we dat eens bekijken voor een Put optie met strike = 105 en premie = 5.

Te zien is dat de put optie geld gaat opleveren wanneer de koers onder de waarde 100 daalt.
Aan de curve zien we dat de verwachting om winst te maken hoger is dan in het plaatje met de Put optie met
strike = 95.
.
We kunnen uit bovenstaande volgende conclusie trekken:
•
Kopen van een optie:
•
Een Call optie long met een strike boven de koerswaarde heeft een lage kans op profit.
•
Een Call optie long met een strike onder de koerswaarde heeft een hogere kans op profit
•
Een Put optie long met een strike boven de koerswaarde heeft een hogere kans op profit
•
Een Put optie long met een strike onder de koerswaarde heeft een lage kans op profit
Vandaar uit kunnen we voorzichtig het volgende plaatje construeren.
Het plaatje is ruwweg, en is bedoeld als een idee / richtlijn.
De witte vlakken vullen we later in.